“Machine learning - Nonsupervised and semi-supervised learning”
Unsupervised learning
Unsupervised learning tries to understand the grouping or the latent structure of the input data. In contrast to the supervised learning, unsupervised training dataset contains input data but not the labels.
Example of unsupervised learning;
Clustering
- K-means
- Density based clustering - DBSCAN
Gaussian mixture models
- Expectation–maximization algorithm (EM)
Latent factor model/Matrix factorization
- Principal component analysis
- Singular value decomposition
- Non-negative matrix factorization
Manifold/Visualization
- MDS, IsoMap, t-sne
Anomaly detection
- Gaussian model
- Clustering
Deep Networks
- Generative Adversarial Networks
- Restricted Boltzmann machines
Self-organized map
Association rule
Semi-supervised learning
In a semi-supervised learning, we use the labeled training data to build a model. However, labeling data is expensive. Instead, we convert non-labeled data to labeled data using the model and combined all data to refit a better model. The purpose of the semi-supervised learning is to augment training data with a model built by the labeled data, so we need far less labeled data than the supervised training.
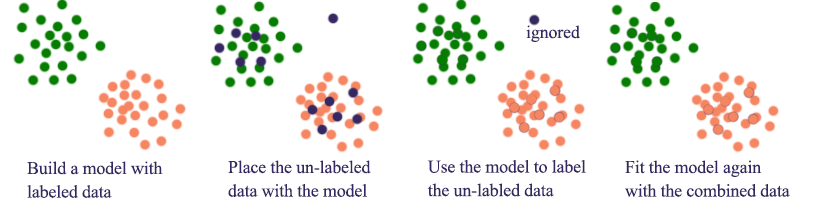
Self-taught training
- Use clustering to fit a model with the labeled training dataset
- Locate the location of the unlabeled data using the model
- Label the unlabeled data
- Combined datapoints to refit the model
- Ignore datapoints that are far from a cluster
However, we do not need to put the same weight on the labeled and unlabeled datapoint. The following cost function uses \(\lambda\) to lower the error cost of the unlabeled data (\(\hat{y}\) and \(\hat{x}\) ) in refitting the model.
\[J(w) = \sum^n_{i=1} \log{(1+e^{-y_iw^Tx_i})} + \lambda \sum^m_{i=1} \log{(1+e^{-\hat{y}_iw^T\hat{x_i}})}\]Co-training
We may have 2 sets of features (\(x_{1s}, x_{2s}\)) that are conditionally independent given the class (\(Y\)). Both feature sets provide different and complementary information.
\[P(x_{1s}, x_{2s} \vert Y) = P(x_{1s} \vert Y) P(x_{2s} \vert Y)\]For example, we may have the spectrogram of a voice clip and its close caption. Can we use them to solve classification problem, say identifying the age group of the speaker?
- Using labeled data, fit one model with the feature set 1 and the second model with the feature set 2.
- Labeled a subset of unlabeled data separately using model 1 and model 2.
- For data that given high confidence in any model, we move the data with the predicted label into our training data set to refit the model.
Co-training works better if one classifier correctly labels a datapoint while the other misclassified it. If both classifiers agree on all the unlabeled data, labeling the data does not create new information. We hope refitting one model with the high confidence data from the other model gives extra information that a stand alone model will not have. Co-training worsened as the dependence of the classifiers increase.
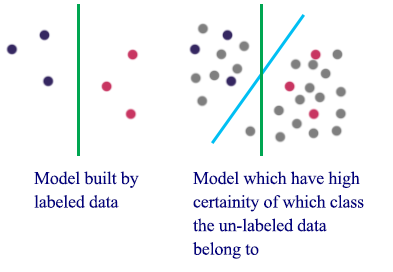
Entropy regularization
Entropy is a measure of random-ness. We want to use labeled data to create a model which the entropy of the unlabeled data to be the lowest. i.e. the resulted model should have high certainty in predicting the labels of the unlabeled data.
Graph based
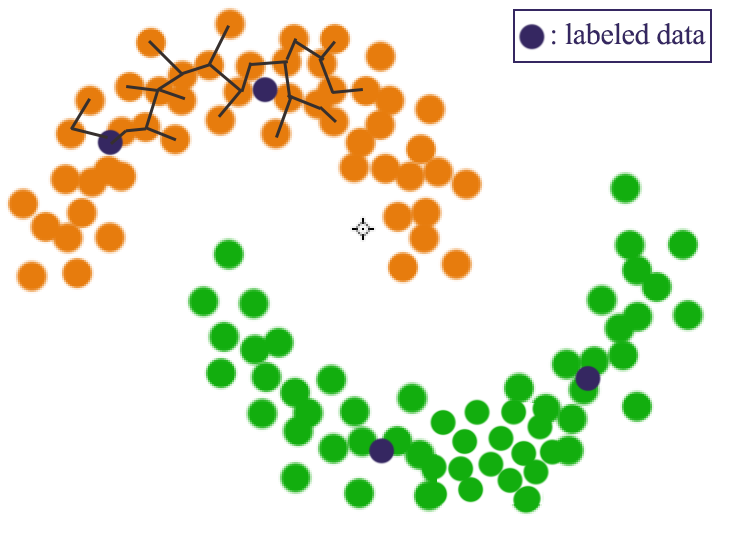
In clustering, DBSCAN connects neighboring high density points together to form a cluster. In semi-supervised learning, we want to connect the labeled data with un-labeled data using density.
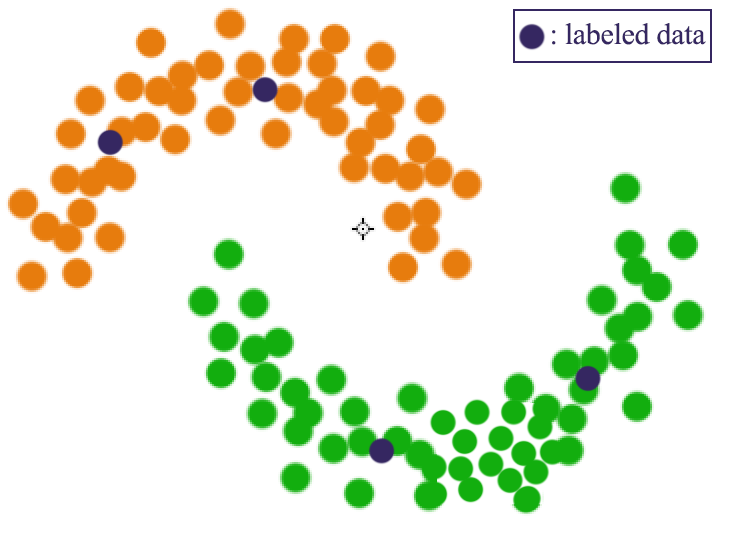
Foe example, we have labeled data \((y_1, \cdots, y_n)\) and unlabeled data \((y_{n+1}, \cdots, y_{n+m})\).
The cost function is:
\[J(\hat{y}) = \frac{1}{2} \sum^n_{i=1} \sum^{n+m}_{j=n+1} w_{ij} (y_i - \hat{y_j})^2 + \frac{1}{2} \sum^{n+m}_{i=n+1} \sum^{n+m}_{j=n+1} w_{ij}(\hat{y_i} - \hat{y_j})^2\]which we want to optimize \(\hat{y}\). The first term in the cost function try to cluster similar labeled and unlabeled data while the second term try to cluster unlabeled data.
\(w_{ij}\) is the graph weight between datapoints:
Markov chain based
We can label data using random walk with a Markov chain model.
- Start at a unlabeled state
- Move to the next state based on the transition probability \(w_{ij}\).
- If the next state has a label, mark the unlabeled datapoint with this label
- Otherwise continue the iteration in the random walk
Credit
Material for semi-supervised learning in this article is based on the class Mark Schmidt’s machine learning class.